What is Binary search explain in hindi

0 Reviews / Post a Review Avaliability Product Avaliable For Sale

algorithms Data Structure

QUICK OVERVIEW:

Add to Cart View Cart Checkout

बाइनरी सर्च क्या है व कैसे काम करता है 

बाइनरी सर्च एक ऐसा तरीका व एल्गोरिथ्म है जिसके द्वारा बहुत सारे डाटा में से किसी एक डाटा को बहुत ही  कम समय में ढूंढ लिया जाता है|

 

वैसे डाटा को सर्च करने के लिए सबसे आसान तरीका है "लीनियर सर्चिंग"| उदाहरण के लिए यदि हमारे पास एक Array है जो कि बहुत बड़ी है व जिसमे बहुत सारे डाटा एलिमेंट्स है| अब यदि इस Array में लीनियर सर्चिंग के द्वारा  किसी एक डाटा को ढूंढना हो तो पूरी Array में हर एक डाटा एलिमेंट को चेक करना होगा| लीनियर सर्चिंग के दौरान हो सकता है कि जिस डाटा को ढूंढ़ना है वे Array की शुरुआत में ही मिल जाए या Array के बीच में कहीं मिल जाए| लेकिन यदि डाटा Array के बिलकुल आखिरी में मौजूद है तो पूरी Array को शुरू से लेकरआखिरी तक चेक करना होगा| इस तरह Array में सर्चिंग में लगने वाला समय Array के साइज के बराबर होगा क्योंकि हर एक डाटा एलिमेंट को चेक करना पड़ता है| ऐरे का साइज जितना बड़ा होगा लीनियर सर्चिंग में लगने वाला समय भी उतना ही अधिक होगा| 

लीनियर सर्चिंग के विपरीत बाइनरी सर्चिंग में लगने वाला समय बहुत कम होता है| बाइनरी सर्चिंग में लगने वाला समय इस फॉर्मूले से निकाल सकते हैं log(n) इसमें n ऐरे में मौजूद डाटा एलिमेंट की संख्या है और इस फॉर्मूले में Log का base 2 है| चाहे सर्च करने वाला डाटा एलिमेंट ऐरे के आखिरी में हो या कहीं भी हो सर्चिंग में लगने वाला समय हमेशा log(n) ही रहता है| 

आइये इसे उदाहरण से समझते हैं एक Array है जिसमे 1000 डाटा एलिमेंट हैं अब यदि इसमें लीनियर सर्च इस्तेमाल की जाए तो इसमें समय लगेगा 1000 लेकिन अगर इसमें बाइनरी सर्च इस्तेमाल किया जाए तो सर्चिंग में समय लगेगा 9.9657 इस उदाहरण से हम समझ सकते हैं कि बाइनरी सर्च बहुत बेहतर है लीनियर सर्च से| अब आइये देखते हैं कि बाइनरी सर्च इंटरनली काम कैसे करता है|       

बाइनरी सर्च एल्गोरिथ्म ऐसे डाटा पर काम करता है जो कि घटते हुए या बढ़ते हुए क्रम में मौजूद हो| अगर डाटा Array में मौजूद है तो ऐरे में डाटा आरोही या अवरोही (Ascending and Descending)  क्रम में होना चाहिए| इसे उदाहरण से समझते हैं मान लेते हैं हमारे पास एक Array है इस तरह :->

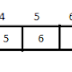
हमें इस ऐरे में 11 डाटा वैल्यू  को सर्च करना है|

बाइनरी सर्च को ऐरे के बीच में से शुरू किया जाता है| ऐरे के बीच का इंडेक्स 5 है तो इस इंडेक्स में मौजूद वैल्यू को सबसे पहले उठाएंगे यहां वैल्यू है 6 अब देखेंगे कि क्या यहां वही डाटा वैल्यू है जिसे सर्च करना है अगर है तो डाटा वैल्यू मिल गयी अगर नहीं तो चेक करेंगे कि इस इंडेक्स में मौजूद वैल्यू सर्च करने वाली वैल्यू से ज्यादा है या कम|

अगर कम है तो अब सर्चिंग ऐरे के 5th इंडेक्स से आगे  के डाटा में करेंगे| अगर ज्यादा है तो सर्चिंग 5th इंडेक्स से पीछे करेंगे| इस केस में 5th इंडेक्स की वैल्यू 11 से कम है इसका मतलब है 11 डाटा वैल्यू ऐरे में 5th इंडेक्स से आगे ही होगा इसलिए अब सर्चिंग 5th इंडेक्स से आगे होगी और 5th इंडेक्स से पीछे की ऐरे में कोई सर्चिंग नहीं होगी|

जैसा कि आप देख रहें हैं पहले स्टेप में ही Array को आधा कर दिया है अब इस आधे ऐरे में ही सर्चिंग करने की जरूरत है|

अब सर्चिंग array के 5th इंडेक्स से लेकर 11th इंडेक्स तक होगी| जो स्टेप्स ऊपर किये गए हैं वही दुबारा किये जाएंगे| 5th इंडेक्स और 11th इंडेक्स के बीच का इंडेक्स लिया जाएगा जो कि है 8 इस इंडेक्स में वैल्यू है 9 अब चेक करेंगे कि क्या यह वैल्यू 11 के बराबर है, बड़ी है या छोटी है| अगर बराबर है तो सर्चिंग खत्म हो गयी| अगर छोटी है तो 8th इंडेक्स से आगे के ऐरे में (9th इंडेक्स से 11th इंडेक्स तक) सर्चिंग करेंगे और अगर यह वैल्यू 11 से बड़ी है तो सर्चिंग 8th इंडेक्स के पीछे के ऐरे (5th इंडेक्स से 7th इंडेक्स तक) में होगी|   

इस तरह हर एक स्टेप में सर्चिंग करने के लिए ऐरे का साइज पहले के स्टेप से आधा होता जाता है जिससे सर्चिंग में लगने वाला समय बहुत ही कम हो जाता है| लेकिन बाइनरी सर्च के लिए यह जरूरी है कि डाटा आरोही या  अवरोही (Ascending and Descending) क्रम में हो|